AB Testing for Email Marketing
- rei-wakayama
- Jan 14, 2024
- 7 min read
Updated: Apr 4
AB testing, one of the simplest forms of a randomized controlled experiment, is basically a way to compare two versions of something to figure out which performs better. These days it’s most often associated with websites and apps. Digital marketing teams can use AB testing to answer questions like which subject line is more likely to get subscribers to open a promotional email, or which image on your website is more likely to get clicked.
Null and Alternative Hypothesis
Before testing, the first crucial step is to clarify your null and alternative hypotheses. The null hypothesis tends to be a statement that your change actually had no effect. For example, your average email open rate was previously 20%, and remains at 20% even after updating the email subject line. Any sample observations resulted purely from chance. The alternative hypothesis would be that your average email open rate is now greater than 20% after the change, influenced by some non-random factor.
Calculate the Required Sample Size
In short, the larger the sample size, the better. Larger sample sizes allow you to be more certain that your test results are truly representative of the overall population.
There are many online tools available such as this one, to calculate your required sample size. You’ll need to prepare the following inputs.
Significance Level: the probability that your result could have occurred by chance, usually set to 5% and denoted by the Greek letter α
Power: the probability of correctly rejecting the null hypothesis when it is false, usually set to 80%.
Baseline Conversion Rate: the current or expected percentage of recipients who will perform the desired action, such as opening an email or clicking on a link.
Minimum Detectable Effect (MDE): The smallest difference between the two versions of the emails that you are willing to detect, expressed as a percentage of the baseline conversion rate.
MDE = (desired conversion rate lift / baseline conversion rate) x 100%Replace “conversion rate” with another metric such as open rate or click thru rate, as needed. For example, if your current average CTR is 5% and the smallest difference that you want to detect is 0.5 percentage points, then your minimum detectable effect is 0.5/5 = 10%.
If you have more than 50,000 subscribers, Salesforce recommends sending to 5% per condition. For example, if your subscriber base is 100,000 and you plan to run a standard AB test to compare 2 different versions of content, you may send version A to 5,000 randomly selected subscribers and version B to 5,000 different subscribers. If you have less than 50,000 subscribers, Salesforce recommends using 10%. If you have a small audience (say, fewer than 500 subscribers) your results may not be statistically significant.
AB Testing in Salesforce Marketing Cloud
This section will briefly cover the best practices when rendering an AB test in Salesforce Marketing Cloud. Other CRM tools may have similar functionality.
AB test for the following elements is available directly in Email Studio: subject line, email, content area, from name, send time, and preheaders. Here, you may also set the criteria to determine the winning email automatically, as either the version with highest unique open rate, or the version with the highest unique CTR.
Email Studio also allows users to define the test distribution, based on either the number of subscribers (i.e. 40 to receive version A, 60 to receive version B) or percentage of subscribers (i.e. 35% to receive version A, 65% to receive version B). The system then randomly splits contacts in the group, according to the user-defined parameters. Note that users cannot control placing a specific subscriber in one distribution or the other.
For more advanced AB tests with 2-10 paths, use the Path Optimizer Test activity in Journey Builder. This is a multi-variant testing tool for testing content, send frequency etc. Once a winner is chosen, either automatically by the system or manually by the user, the winning path will continue to receive new contacts while the losing path(s) will stop taking in new contacts, allowing for journey optimization. The Path Optimizer test activity also provides test summary analytics, including historical test context for decision making.
When using Journey Builder for AB tests, consider including a Validation activity as well. Validation confirms that the journey's components are working correctly, by checking for errors or configuration issues in the following activities: entry source, entry schedule, decision splits, wait activities, update contact activities, email engagement splits, journey settings, journey goals and exit criteria.
Don't forget that although you are AB "testing", the emails are still being sent to real subscribers. Promotional emails should always comply with CAN-SPAM requirements and Marketing Cloud's Anti-Spam policy.
Finally, note that if your AB test involves email open rates, note that Apple’s Mail Privacy Protection released in September, 2021 may cause your open rate data to be inflated and skew results.
How to Measure Statistical Significance
Statistical significance measures how likely it would be to observe what was observed, assuming the null hypothesis is true. In other words, statistical significance means that if you were to run the test again, you should get the same result. There are actually two ways to determine whether your test results are statistically valid.
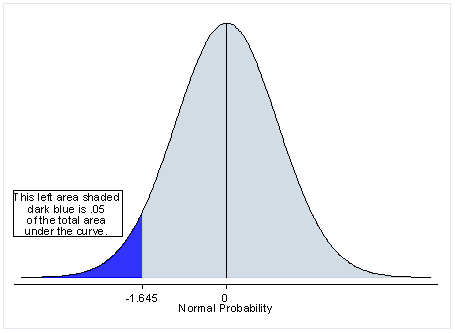
One-tailed tests (top image) allow for the possibility of an effect in one direction, and show evidence if the variation is better than the control. In a one-tailed test, the null hypothesis is that the variation is not better than the control, but could be worse. The two-tailed test (bottom image) allows for the possibility of either a positive or negative effect, and shows evidence if the variation and control are simply different.
In the real world, I generally go with a two-tailed test for most cases of AB testing. I often don’t know the direction of difference in key metrics, and it’s totally possible that the new variation performs worse. One-tailed test may also be fine if you’re testing a new variation and only want to know whether it is better than the control or not. If you don’t plan to deploy the new variation if it doesn’t win, then there is no problem. However, there could be a problem if there is no statistically significant winner and you deploy the new variation by assuming that it didn’t perform worse.
Assuming that AB tests for digital marketing have large sample sizes, use z test to analyze the results. Under the Central Limit Theorem, the sample is expected to have a normal distribution, and you don't have to worry about normality. In my experience, most people don't actually check the sample distribution if they have reasonable confidence that the assumptions for using z test are true. To determine the statistical significance of your completed AB test, check the following values.
Z score: how many standard deviations away from the mean your result lands, in a normally distributed sample.
Z score = (Data Value - Mean) / Standard DeviationStandard error: the standard deviation of a sample population, used to measure the accuracy with which the sample represents the whole population.
Standard Error = SQRT {P*(1-P) / Sample Size}Standard Error = Standard Deviation / SQRT(Sample Size)P value: the probability of getting your result, assuming that the null hypothesis is true. Use the following Excel function to find the p value from z score.
= NORMDIST(z score, mean, standard deviation, cumulative)* mean: the mean of the distribution, use 0 for standard normal distribution
* standard deviation: use 1 for the standard normal distribution
* cumulative: "FALSE" returns the probability density function, the probability distribution of a continuous random variable; "TRUE" returns value of the cumulative distribution function, the probability distribution of both discrete and continuous random variable
If the p value is less than your significance level, reject the null hypothesis. It means that there’s sufficient evidence of the alternative hypothesis. Otherwise, fail to reject the null hypothesis.
Type I and Type II Errors
Type I error is a false positive, meaning that you falsely concluded that any variation of an AB outperformed the other(s) with statistical significance. The probability of a Type I error is the significance level of your AB test. So if your test result has 95% confidence level, your probability of a Type I error is 5%.
Type II error on the other hand, implies a false negative. In other words, Type II error falsely concludes that there is no statistically significant difference between the variations in your AB test, when there actually is a difference. Type I and Type II errors have an inverse relationship - by increasing your confidence level, the probability of Type I error decreases, and the risk of a Type II error increases.
Many organizations view AB test outcomes as trustworthy enough to influence their business decisions. It's generally not necessary to repeat a test, unless something went wrong or the environment has changed. So when running AB tests, always record not only the test results, but also the environment that you ran it in - what was the state of any relevant elements of your product and customers?
Limitations of AB Tests for Email Marketing
The biggest limitation is probably that AB testing looks at dependent variable results without considering the interactions of independent variables, so you can only make one change at a time. If you don't have enough time to test this way, or you're changing multiple variables and want to know more about which change mattered, it's time to look at multivariate testing instead. Multivariate testing is a more complex version of traditional AB testing. With multivariate testing, you can investigate further into the interactions of multiple independent variables on the target dependent variable.
Finally, an abstract point to end this post... as long as humans are conducting data analysis, there will be some level of cognitive bias involved. In layman's terms, the Dunning Kruger Effect means that "the less competent you are, the more confident you tend to be." Basically, people who are unskilled suffer a dual burden: they tend to reach erroneous conclusions and miss key insights, and on top of that, their incompetence robs them of the metacognitive ability to realize it in the first place.




Comentarios